La estructura física de un disco rígido esta compuesta por:
Cabezas lectoras que recorren la superficie del disco
Platos que son pequeños discos que se encuentra uno sobre otro y compuestos por caras.
Las pistas que son circuferencias ubicadas en una cara.
Y cilindros definidos como la unión de pistas alineadas verticalmente.
Una correcta planificación trae con sigo un aumento en la velocidad de acceso a datos:
Planificación FCFS Conocido como first-come-fist-served es un algoritmo que atiende las peticiones en orden de llegada sin importar si se encuentran en ragos muy dispersos. No es muy eficiente pues el cabezal de lectura recorre la superficie de una manera irregular.
Planificación SSTF Basada en el principio de short-seek-time-first estable las peticiones de dirección de tal manera que será atendida aquella que se encuentre más cerca de la cabeza de lectura. Este algoritmo reduce considerablemente el tiempo, pero como desventaja puede provocar que inanición por la presencia de solicitudes siempre menores.
Planificación SCAN También conocido como algoritmo del elevador, pues recorre toda la longitud de los platos de un lado a otro buscando en su camino las solicitudes que se encuentren pendientes. Uno de sus inconvenientes es el que las solicitudes de acceso no tienen un tiempo de espera uniforme, es decir, las de un extremo serán atendidas luego de un tiempo mayor.
Planificación C-SCAN Esta planificación es una variación del anterior que resuelve la espera de tiempo para cada solicitud, haciendo un recorrido uniforme en cuanto ha atender pedidos lo que hace que la cabeza lectora recorra el plato de inicio a fin y retorne.
Planificación LOOK En la práctica los dos algoritmos anteriores, que recorren todo el plato no son implementados, si no que se usa más la forma de detectar la última petición y regresar nuevamente al principio, es decir no hay razón de seguir recorriendo si ya no existen solicitudes.
Otro aspecto importante en el almacenamiento masivo:
Espacio de Intercambio Este es un concepto importante pues su implementación es conocida como memoría virtual. Lo quepermite aumentar la cantidad de memoría de tal manera que el SO moverá al disco todo o parte de un proceso sin mucha actividad, permitiendo liberar recursos.
Para ubicar el espacion de intercambio existen dos formas, la primera como un fichero de intercambio que puede reducir o ampliar su tamaño pero que puede ser afectado por la paginación y la segunda una Partición de intercambio, que es basicamente especificar una partición del disco para utilizar, y en diferencia a la anterior no puede ser modificado su tamaño.
ARRAYS (ARREGLOS)
Un array (también llamado arreglo) es una agrupación de muchos datos individuales del mismo tipo bajo el mismo nombre. Cada dato individual de un array es accesible mediante un índice.
VECTOR Es el caso más simple de array unidimensional.
En los vectores hay dos cosas que hay q diferenciar y son:
Posición y la cantidad.
Por ejemplo: int serie[5]=3;
La cantidad es 3 y la posición es 5. En la posición 5 del vector serie. se almacena el número 3.
Los vectores siempre arrancan de la posición 0.
OPERACIONES BASICAS CON VECTORES
Manipulación de elementos individuales Los vectores en C deben manipularse elemento a elemento . No se pueden modificar todos los elementos a la vez.
Llenado de un vector por definición: Para asignar valores a los elementos de un vector, por lo tanto, el mecanismo es este:
int serie[5];
serie[0] = 5;
serie[1] = 3;
serie[2] = 7;
...etc...
La inicialización de los valores de un vector también puede hacerse conjuntamente en el momento de declararlo, así: int serie[5] = {5, 3, 7, 9, 14};
El resultado de esta declaración será un vector de 5 elementos de tipo entero a los que se les asigna estos valores:
Cada elemento del vector es, a todos los efectos, una variable que puede usarse independientemente de los demás elementos. Así, por ejemplo, un elemento del vector serie puede usarse en una instrucción de salida igual que cualquier variable simple de tipo int: int serie[5];
serie[0] = 21;
printf("%i", serie[0]);
Del mismo modo, pueden usarse elementos de vector en una instrucción de entrada. Por ejemplo:
int serie[5];
scanf("%i", &serie[0]);
serie[1] = serie[0] + 15;
printf("%i", serie[1]);
Llenado de un vector por lectura o teclado:
int v[n]=0, i;
for (i=0; i<=n-1, i++)
{
printf (datos:%d : ,i+1);
scanf ("%d",v[i] );
}
Imprimir un vector
for (i=0; i<=n-1, i);
printf (datos:%d : ,i+1);
Sumar posiciones
a=0;
for (i=0; i<=n-1, i++)
printf (datos:%d : ,i+1);
a=a+v[i];
COMO ORDENAR UN VECTOR
Mencionaremos tres métodos de ordenación muy populares:
1. Ordenación por INTERCAMBIO DIRECTO (burbuja) El método de la burbuja es muy ineficiente, pues tarda mucho tiempo en ordenar un vector si éste es muy largo. Pero es fácil de entender.
La idea general es simple: tomaremos los dos primeros elementos y los compararemos. Si están desordenados, intercambiamos sus posiciones. Si están ordenados, los dejamos como están.
Después haremos lo mismo con los elementos segundo y tercero (comparar y, si es necesario, intercambiar). Luego, con el tercero y el cuarto. Después con el cuarto y el quinto, y así sucesivamente hasta recorrer el vector completo.
Cuando lleguemos al final, el vector no estará todavía ordenado, pero el elemento más grande del vector habrá subido hasta la última posición, igual que una burbuja de aire en el agua .
Si volvemos a repetir el proceso desde el principio, el segundo elemento más grande habrá subido hasta la penúltima posición del vector. Y, la siguiente vez, el tercer elemento más grande subirá hasta la antepenúltima posición. Y así hasta que ordenemos todos los elementos.
Si el vector tiene N elementos, hay que repetir el recorrido N veces, aunque en cada repetición podemos quedarnos una posición más abajo del final, ya que sabemos con seguridad que los últimos elementos están colocados en su sitio.
El algoritmo funciona exactamente igual si recorremos el vector desde el final hacia el principio, sólo que, en ese caso, son los elementos más pequeños los que van descendiendo y colocándose en su posición definitiva en cada iteración del algoritmo.
void ordena_vector(int v[longitudvector])
{
int i, j, minimo, posicion_minimo;
for (i = 0; i < minimo =" v[i];" posicion_minimo =" i;" j="i;" minimo =" v[j];" posicion_minimo =" j;">
2. Ordenación por selección directa El algoritmo de selección directa también parte de un concepto bastante simple: es recorrer todo el vector para buscar el elemento más pequeño y, una vez localizado, colocarlo en la primera posición.
El elemento que estuviera ocupando la primera posición debe ser movido al lugar donde estaba el elemento más pequeño, claro, o de lo contrario se sobreescribiría y se perdería para siempre.
Después, haremos lo mismo buscando el segundo elemento más pequeño, moviéndolo a la segunda posición del vector. Luego buscamos el tercer elemento más pequeño, el cuarto, etc. Repitiendo esta búsqueda tantas veces como elementos tenga el vector, habremos conseguido ordenarlo.
A continuación se presenta una posible implementación en C.
Observe que también se necesitan dos bucles anidados para culminar el proceso, por lo que el número de pasos necesarios es alrededor de N 2 y, por lo tanto, el tiempo de ejecución también crece exponencialmente, como en el caso de la burbuja.
void ordena_vector(int v[LONGITUD_VECTOR])
{
int i, j, elem;
for (i = 1; i <>
{
for (j = LONGITUD_VECTOR - 1; j >=i; j--)
{
if (v[j-1] > v[j])
{
elem = v[j-1];
v[j-1] = v[j];
v[j] = elem;
}
}
}
}
Ordenación rápida (QUICKSORT) El algoritmo Quicksort (u ordenación rápida) es un método de ordenación mucho más elaborado que los dos anteriores y, por lo tanto, más difícil de comprender. La versión que presentamos es recursiva, pero existen implementaciones equivalentes iterativas, más difíciles (todavía) de comprender, pero más rápidas.
El proceso de intercambio de pares se repetirá hasta que alcancemos el pivote. Entonces, sabremos que todos los elementos de la derecha del pivote son mayores que éste, y, los de la derecha, son menores.
Ahora dividimos el vector en dos mitades: a la izquierda del pivote y a la derecha del pivote. Procesaremos cada mitad con el mismo procedimiento: buscar un nuevo pivote e intercambiar elementos de la izquierda y de la derecha.
Repetiremos el proceso hasta que los vectores sean triviales (es decir, hasta que el pivote coincida con los extremos izquierdo y/o derecho).
Este algoritmo necesita, por término medio, un número de pasos proporcional a N * log(N). Puede que no parezca mucho comparado con el N 2 que necesita la burbuja, pero, para tamaños muy grandes, la diferencia de tiempos es enorme.
NOTA: en esta implementación, por simplicidad, el vector v es una variable global
void ordena_vector(int iz, int de)
{
int i, j, x, w; i = iz;
j = de;
x = v[(iz+de) / 2];
do
{
while (v[i] < w =" v[i];" w =" v[i];">
MARTINEZ B, Néstor Raúl. METODO BURBUJA EN VECTORES . Universidad Cooperativa de Colombia seccional Bucaramanga, 2009 ó en el cd de la tesis en la ruta CD DE LOGICA DE PROG\VIDEOS BLOGGER LOGICA DE PROGRAMACION
MATRICES
Una matriz, tabla o array bidimiensional, como un vector, es una colección de elementos individuales, todos del mismo tipo, agrupados bajo el mismo identificador. La diferencia con el vector es que, en el momento de declararlo y de acceder a cada elemento individual, debemos utilizar dos índices en lugar de uno:
int matriz[4][4];
Cada casilla de la tabla o matriz es identificable mediante una pareja de índices. Normalmente, el primero de los índices se refiere a la fila, y el segundo, a la columna. Por ejemplo, si hacemos estas asignaciones:
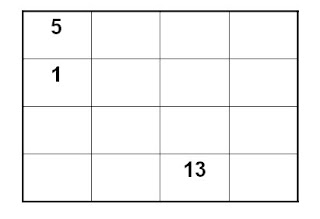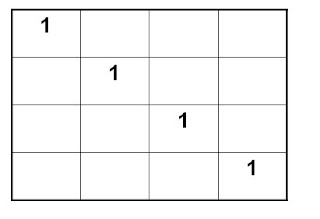
Por descontado, los dos índices de la matriz pueden ser diferentes, obteniéndose tablas que son más anchas que altas o más altas que anchas.n = Filas y m = Columnas.
int A[n][m]={{3,7,4,2},{1,1,1,1},{3,5,8,9},{4,3,7,8},{6,2,3,4} }
for (i=0; i<=n-1, i++)
for (i=0; i<=n-1, i++)
for (i=0; i<=n-1, i++)
for (i=0; i<=n-1, i++)
Suma por filas
float s[n]=0;s[i]=suma;
for (i=0; i<=n-1, i++)
Imprimir la suma de las columnas
printf ("%f", A[i][j]);
j=1;
printf ("%f",A[i][j]);
MARTINEZ B, Néstor Raúl.SUMA DE FILAS Y DE COLUMNAS EN UNA MATRIS DE MxN. Universidad Cooperativa de Colombia seccional Bucaramanga, 2009 ó en el cd de la tesis en la ruta CD DE LOGICA DE PROG\VIDEOS BLOGGER LOGICA DE PROGRAMACION
No hay comentarios:
Publicar un comentario